What are Critical Loads?
A critical load has been defined by Nilsson and Grennfelt as ‘a quantitative estimate of the exposure to one or more pollutants below which significant harmful effects on specified sensitive elements of the environment do not occur according to present knowledge’.
In other words, the level of input below which damage to the tree, soil or ecosystem is thought unlikely is known as the critical load. Where a critical load is exceeded, it does not always mean that damage will occur. Critical loads are set to protect ecosystems in the long term; the effects of pollutants can take many decades to appear, and thus if damage does occur, it is may not be immediately apparent.
Critical loads are set for:
Forest critical loads are set to protect specific receptors. We are working to develop critical loads for woodland that are appropriate to both the semi-natural woodland and forest management practices adopted in the UK.
Policy relevance
The critical load approach is a key element of emissions reduction policy. It has proved to be very useful in policy development since its ‘effect based’ approach allows the environmental benefits of emission reductions to be evaluated. The critical loads approach has been adopted by the UNECE Convention on Long Range Transboundary Air Pollution (CLRTAP) to target pollutant reduction targets and it is now one of the main drivers of emission control agreements under the UNECE CLRTAP, the EC European Acidification Strategy, and Clean Air for Europe.
Soil sustainability – Critical loads for heavy metals
The critical load for heavy metals depends on the acceptable total load of anthropogenic heavy metal inputs (deposition, fertilisers, other anthropogenic sources), below which ecosystem damage is unlikely.
Critical loads methods for toxic metals are currently being developed within the United Nations Economic Commission for Europe (UN/ECE) Convention on Trans-boundary Air Pollution (CLRTAP). In the UK, a research consortium currently contributes both to the development and the improvement of the critical loads method for application within the UN/ECE and to the development of improved tools to assess the effects of changing rates of atmospheric deposition on pools of metals in soils and freshwaters. Forest research is a sub-contractor to this consortium and have contributed to the calculation, evaluation and update of critical loads for heavy metals for forest ecosystems in the UK.
Effects-based steady-state and stand-still critical load approaches have been used for heavy metals critical loads calculations and mapping.
Effects-based steady-state critical loads: CLeffb(M)
The steady state equation for the calculation of heavy metal critical loads is as follows:
CL(M) = Mu – Mw + Mle(crit)
Where:
CL(M) is the critical load of heavy metal M.
Mu is the removal of heavy metals by biomass harvesting or net uptake in forest ecosystems from the mineral topsoil.
Mw is the weathering release of heavy metals from the mineral top soil,
Mle(crit) is the critical leaching of heavy metals from the mineral top soil, in which only the vertical drainage flux is considered.
Growth uptake values are calculated from estimates of average annual biomass increment multiplied by the content of the metal in the tree. Previous uptake values for woodland have been derived from a default range of metal concentrations in trees (UBA, 1998), and average yield data. New uptake values for heavy metals (Cu, Zn, Cd, Pb, Ni and Cr) are now available based on the measurements from the twenty Level II Intensive Monitoring sites in the UK and will be used in future modelling.
For the UK, the model has been simplified by removing the weathering term because the input of metals by weathering was considered negligible compared to metal deposition, while the uncertainties associated with such calculations are high. The approach described here implies that the critical load equals the net uptake by forest growth plus an acceptable metal leaching rate.
The ‘critical limit’ defines an acceptable maximum concentration of a metal below which long term deleterious effects to an ecosystem should not occur. Thus, defining the ‘critical limit’ is crucial to the critical load approach. For lead (Pb) and cadmium (Cd), ‘critical limits’ of 8 mg/m3 and 0.8 mg/m3 respectively have been adopted.
The depth considered in the calculation is 10 cm for forest soils or the depth of the A horizon, since impacts on plants and soil organisms, which are the main target groups considered are largely restricted to this depth.
Stand – still critical loads: CLstst(M)
The critical load equation used for the standstill approach is the same as for the effect based steady-state method, but with the ‘critical limit’ being replaced by the ‘concentration of metal’ in the soil solution, on the premise that no further metal accumulation will be allowed.
In brief an ‘effect based’ methodology, identifies atmospheric deposition (critical loads) that will not lead to concentrations of heavy metals above critical limits in defined compartments at steady-state. These critical loads can be derived using:
- Critical limits of heavy metal concentrations in the soil solution which will not harm microbiota and plants and/or
- Critical limits of (reactive) soil metal concentrations which will not lead to adverse impacts on soil functioning, such as soil invertebrates that ingest soil.
‘Stand-still’ critical loads equal the atmospheric deposition that will not lead to any further accumulation of heavy metals in the soil. In fact, stand-still critical loads should also include inputs other than atmospheric deposition.
A limitation of the ‘stand-still’ approach is that data on current concentrations of heavy metals in soil solution are scarce. Leaching can therefore only be mapped on the basis of ‘transfer functions’ which convert total content of metals in the upper soil horizon into concentrations in soil solution. ‘Transfer functions’ are available which describe the relationship between dissolved and adsorbed concentrations of heavy metals, accounting for the impact of soil properties such as pH and organic carbon content.
Previously, the critical loads models have only been applied to upland forests. Recently, the critical loads models have also been applied nationally to lowland forests,
Preliminary modelling and mapping of critical loads for cadmium and lead for upland forested areas suggest that the soil solution concentrations exceed the critical limits (ie, Pb 8 mg/m3, Cd 0.8 mg/m3) in some upland areas of England, Wales and Northern Ireland, with the critical limit for Pb exceeded in 41% of grid squares. For Cd, the critical limit is exceeded in 17% of grid squares.
However, there are still major uncertainties concerning the most appropriate methodological approaches to be used when applying the critical load concept to metals, as opposed to acid deposition. Further research will test the approaches to heavy metal critical loads mapping, applying site-specific soil water chemistry, heavy metal deposition and estimates of heavy metal uptake.
Useful sites
Soil sustainability – Acidity and nutrient nitrogen critical loads and exceedance for woodland habitats
The continuous evaluation and development of the critical loads methodology using current data is crucial for targeting implementation policies towards effective ecosystem recovery. For woodland, the approach must be appropriate to the breadth of environmental conditions and woodland types present in the UK, and also representative of both unmanaged woodland and current practices employed across the managed forest estate.
Woodland habitat mapping
Managed and unmanaged woodland have been mapped separately by combining three woodland cover maps from different sources. The managed woodland category has been further categorised into conifer and broadleaf woodland to enable critical load exceedances to defined receptors for each woodland type to be mapped.
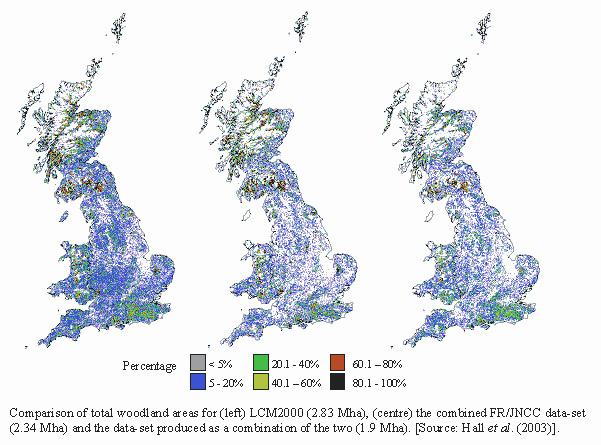
For acidity, the ‘broadleaved, mixed and yew woodland’ Broad Habitat is sub-divided into two categories :
- Managed (productive) broadleaved woodland
- Unmanaged (ancient & semi-natural) coniferous and broadleaved woodland.
For nutrient nitrogen, the unmanaged woodland is further divided into ‘Atlantic oak woods’ (for the effects of nitrogen on epiphytic lichens) and other ‘unmanaged woodland’ (for the effects of nitrogen on ground flora).
The coniferous woodland broad habitat only includes managed coniferous woodland. The unmanaged coniferous areas are included in the unmanaged (ancient & semi-natural) coniferous and broadleaved woodland category because the receptor (ground flora) and critical load are the same in both.
The unmanaged woodland category consists of ancient and semi-natural woodland, yew and Scots pine and is ‘managed’ for biodiversity or amenity, but not timber production. All other coniferous and broadleaved woodland is assumed to be primarily managed as productive forest where harvesting and removal of trees takes place. Both managed and unmanaged woodlands are included, since the long-term protection of the whole ecosystem function is important.
Acidity Critical loads for woodland
The methods used to calculate acidity critical loads for woodland habitats differ according to the soil type dominant in the 1km grid square in which the woodland occurs. For mineral and organo-mineral soils, critical loads are based on the Simple Mass Balance (SMB) equation and a critical molar ratio of calcium to aluminium (equal to 1.0) in soil solution. Critical loads of acidity for peat soils are based on a critical soil solution pH value of 4.4.
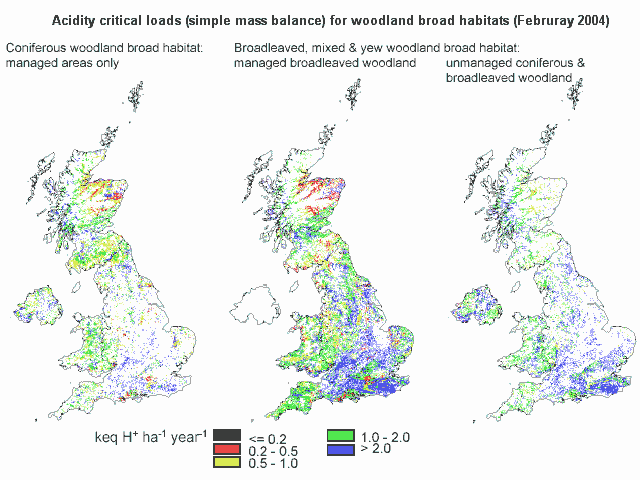
A detailed explanation of the latest changes made to the methods and criteria for the calculation and mapping of critical loads can be found in Hall et al., 2004 (The United Kingdom National Focal Centre – UK NFC).
Nutrient nitrogen critical loads for woodland
The critical loads for nutrient nitrogen for woodland, used for UK mapping, have been revised in the light of the conclusions of the Berne workshop (PDF-673K) in November 2002. The Berne workshop, proposed a single nutrient nitrogen critical load value for forests of 10-20 kg/ha/yr, as quite reliable, and suggested that national experts use broad guidance on modifying factors to decide on national mapping values. However, an approach based on specific response variables was considered to be more appropriate for use in the UK. These responses, for defining critical loads in the UK are the effects on:
- Nitrate leaching
- Ground flora
- Epiphytic lichens and algae.
The critical loads for managed conifer plantations are set to protect the soil on the basis that there is little ground vegetation present under most managed conifer plantations in the UK. Furthermore, it is likely that management practices will have more impact on the vegetation than pollution inputs. A summary of the nutrient nitrogen critical loads for the different woodland habitats is shown in Table 1. Empirical and Steady state mass balance approaches are used for their calculation. Further details are given in Hall et al., 2003 (UK NFC).
Table 1. Summary of empirical critical loads for nitrogen (kg/ha/yr) for forests
| Woodland habitat |
Critical load methodology |
Critical load |
Receptor |
| Unmanaged woodland |
Empirical |
12 |
Ground flora |
| Managed conifer |
Steady state mass balance approach |
12 |
Soil ecosystem |
| Managed broadleaf |
Steady state mass balance approach |
12 |
Ground flora |
| Atlantic oakwoods |
Empirical |
10 |
Epiphytic lichens |
Critical loads exceedance
Critical load exceedance maps for nutrient nitrogen and acidity now account for forest management activities (thinning, harvesting and fertilisation) that can affect nitrogen and base cation removal or addition through growth uptake. This is achieved though the uptake term in the Simple Mass Balance equation based on growth estimates and nutrient concentration measurements made across the Level II network. These datasets have recently been updated.
Nutrient nitrogen exceedance maps
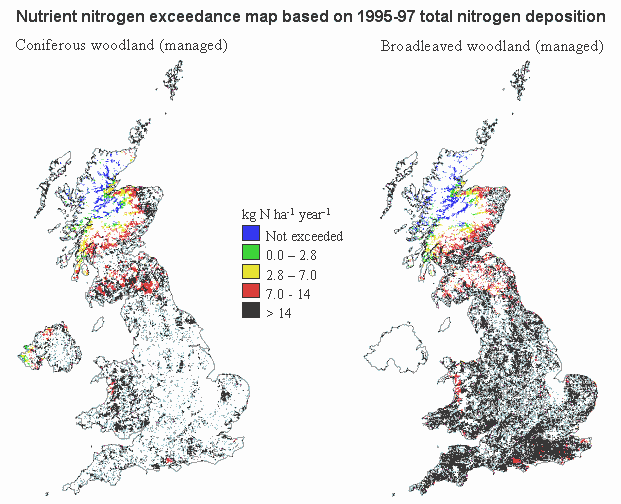
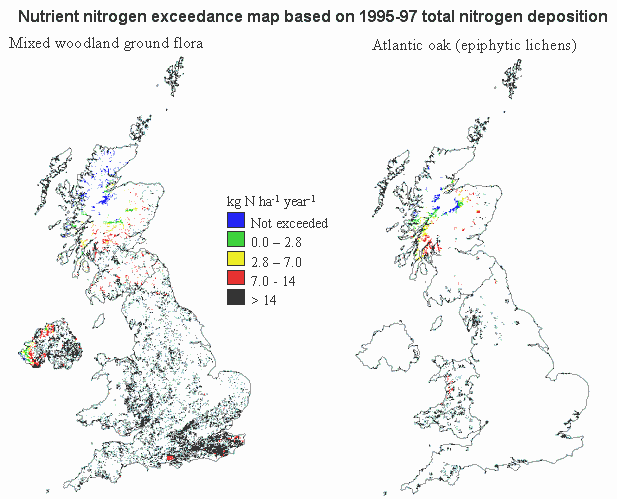
Acidity exceedence maps
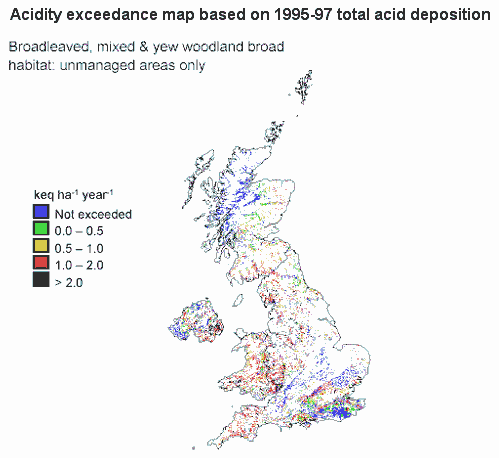
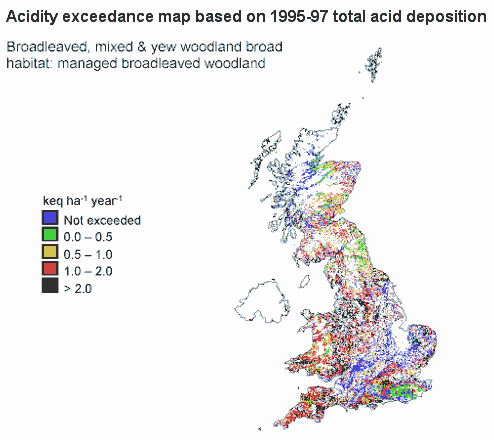
The latest UK statistics on the percentage of habitat area exceeded for acidity and nitrogen is shown in Table 2.
Table 2. UK statistics on the percentage of habitat area exceeded for acidity and nitrogen based on the updated 2004 critical loads and the latest version of deposition data for 1999-2001 (Hall et al. 2004)
| Woodland habitat |
2004 % habitat area exceeded |
| Acidity |
Nitrogen |
| Conifer woodland (managed) |
70.5 |
92.8 |
| Broadleaved woodland (managed) |
69.1 |
97.8 |
| Unmanaged woodland |
58.6 |
95.8 |
Are our forests endangered by acid and nitrogen deposition as suggested by the critical load approach?
The latest critical load exceedance statistics indicate that between 50 and 70% of the UK’s woodland area is growing under excessive acidity deposition and between 93 and 97% for nitrogen (see Table 2). The critical load exceedance is based on calculated critical loads and current acid deposition.
The acidity critical loads are set to protect the soil while the nitrogen critical loads are set to protect the ground flora. Therefore tree growth and health are not the receptor defined in the UK approach to critical loads mapping. When steady-state critical loads are compared to deposition two outcomes are possible:
- The deposition is below the critical loads, which implies that there is no critical load exceedance; there is no risk to the ecosystem and a reduction in deposition is not necessary
- The deposition is above the critical load and thus critical load exceedance is apparent; there is a risk for damage to the ecosystem and reduction of deposition is necessary.
It is often assumed that a reduction in deposition will immediately remove the risk of harmful effects to the ecosystem. However, the response of soils, especially their solid phase, to changes in deposition may be delayed by decades or even centuries as a result of (finite) buffers, the most important being the cation exchange capacity. These finite buffers are not included in the critical load formulation, since they do not influence the steady state, but only the time to reach it. Calculations using exchangeable cations in the soil and the steady state critical load exceedance can be used to estimate the time-frame expected for detrimental effects on tree health to be observed.
For three Level II plots, this time was calculated (Kennedy et al., 2001) to be:
- 1187 years for Alice Holt (Oak)
- 66 years for Grizedale (Oak)
- 13 years for Ladybower (Scots pine)
There is generally a time lag between a chemical change and a biological response. The same is true when an ecosystem recovery from excessive pollution loading is expected. Thus, the critical loads can be used as a measure of potential damage but not as a measure of damage that has already occurred. Dynamic models are now used to predict the time-frame over which damage to forest ecosystems is expected.
High variability in nitrogen deposition to forests is also evident. Critical load exceedance statistics are based on a 5 km grid. Nitrogen deposition can vary greatly over this area, potentially introducing an overestimation in the area exceeded. At the same time, the extent of exceedance at woodland edges will be underestimated. Another area of uncertainty is that where much of the N loading is derived from ammonium deposition, this nitrogen load is likely to be smaller to the ground flora as a result of uptake by the overstorey. Thus, nitrogen critical loads exceedances needs to be interpreted with caution.
Further research will improve the uncertainties associated with critical load calculations and exceedances.
What’s of interest
About the maps
The maps on this page have been provided by Centre for Ecology & Hydrology
Related pages
Useful sites
Soil sustainability – Critical loads methodologies
The methods for calculating critical loads are based on internationally agreed approaches and have been adapted to make use of national data sets that are available for producing UK maps. The methods currently used in the UK to calculate acidity and nutrient nitrogen critical loads are summarised below:
Critical loads of acidity: Simple Mass Balance (SMB) equation
The critical loads for acidity are designed to protect the soil. The SMB equation is used for calculating acidity critical loads for woodland ecosystems. The SMB method provides critical loads for systems at steady-state. This model is based on balancing the acidic inputs to and outputs from a system, to derive a critical load that ensures a critical chemical limit (related to effects on the ecosystem) is not exceeded. The equation has been derived from a charge balance of ions in leaching fluxes from the soil compartment, combined with mass balance equations for the inputs, sinks, sources and outputs of sulphur and nitrogen. The simplified equation between the sources and sinks of sulphur and nitrogen is:
Sdep + Ndep = BCdep – Cldep + BCw – BCu + NI + Nu + Nde – ANCle
Where:
BC = the sum of base cations (Ca+Mg+K+Na).
Subscripts dep, le, w, u, i and de represent deposition, leaching, weathering, uptake, immobilisation and denitrification processes.
ANCle = the leaching of Acid Neutralising Capacity.
The simplified mass balance equation is converted to a critical load equation by the addition of the ‘biological limit’:
CL (S + N) = CL(S) + CL(N) = BCdep – Cldep + BCw – BCu + NI + Nu + Nde – ANCle(crit)
Where:
CL(S), CL(N) and CL(S+N) represent the critical loads of sulphur, nitrogen and sulphur plus nitrogen, respectively.
ANCle(crit) = the leaching of Acid Neutralising Capacity with the addition of the biological limit denoted as crit. Further details of how this is calculated are given by the United Kingdom National Focal Centre (UK NFC).
If sulphur deposition is zero, then the equation above becomes the maximum critical load of acidifying nitrogen CLmax (N). However, if nitrogen deposition is zero, then the equation above is not the maximum critical load of sulphur because nitrogen acidity sinks cannot compensate for incoming sulphur acidity. Therefore, the CLmax (S) is defined as:
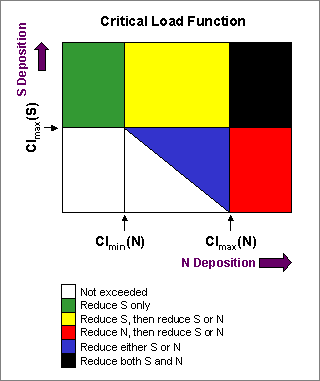
The SMB equation is parameterised according to the appropriate critical chemical criteria and critical limits that will protect the receptor (soils) from the adverse effects of acidification. A critical molar ratio of calcium to aluminium of one in soil solution is a common criterion applied in the SMB to protect the fine roots of trees. This criterion is used for mineral and organo-mineral soils. In the case of peat soils, critical loads of acidity use a critical soil solution pH value of 4.4.
Most tree species grow well in soils of considerable lower pH. However, a critical soil solution pH of 4.4 was set to protect soils to enable future non-woodland land use and possible reversion to semi-natural vegetation. Further investigation of pH values of pristine peat soils is currently in progress.
In the UK, the SMB equation is applied to all woodland ecosystems including both managed and unmanaged woodlands.
Critical Loads of nutrient nitrogen
Enhanced nitrogen deposition to forest ecosystems can lead to acidification or eutrophication. The latter can have major impacts on plant communities leading to changes in species composition and the sensitivity of vegetation to environmental stresses such as drought, frost or insect predation. Therefore, methods have been developed to set critical loads to protect against these adverse effects. Two approaches are currently in use: empirical and mass balance; both methods are described, briefly, below.
Empirical critical load for nutrient nitrogen
Empirical nutrient nitrogen critical loads are based on the results of experimental studies and field observations, or on ‘expert judgement’.
Ranges of critical load values are given to take account of:
- Inter-ecosystem variability due to factors such as climate and management practice
- The range of experimental treatments where an effect was observed or not observed
- Uncertainties in deposition values where critical loads are based on field observations.
The ranges of critical load values recommended are also accompanied by one of the following ‘reliability’ scores:
- ‘Reliable’ – where a number of published papers of various studies show comparable results
- ‘Quite reliable’ when the results of some studies are comparable
- ‘Expert judgement’ or ‘informed estimate’ where no data are available for a particular ecosystem type.
Empirical critical loads for unmanaged woodland ecosystems are set to protect the woodland ground flora from adverse effects, rather than to protect the trees themselves. Atlantic oakwoods are a special case, with a lower empirical critical load set to protect the epiphytic lichen community.
Mass balance critical loads for nutrient nitrogen
The steady state mass balance for nutrient nitrogen is calculated as:
CLnutN = Nu + Ni + Nle(acc) + Nde
Where:
Nu = nitrogen uptake
Ni = nitrogen immobilisation
Nle(acc) = acceptable level of nitrogen leaching
Nde = denitrification
This method is based on the above equation, which balances all significant long-term inputs and outputs of nitrogen for terrestrial ecosystems, assuming that the system is at equilibrium. In this context, long-term is defined as at least one forest rotation or 100 years. Critical loads calculated using this method are set to:
- Prevent an increase in leaching of nitrogenous compounds, particularly nitrate, which may result in damage to the terrestrial or, linked, aquatic systems
- Ensure sustainable production by limiting nitrogen uptake and removal to a level which will not result in deficiencies of other nutrients.
In the UK, the mass balance equation has been used to calculate nutrient nitrogen critical loads for managed coniferous and deciduous woodland ecosystems. The national maps are currently based on the minimum of the empirical or mass balance critical load values.
Calculation and mapping of critical load exceedances
Critical loads are compared with acidifying or eutrophying deposition to determine the excess deposition above the critical load; ie the exceedance.
Exceedance = Deposition – Critical Load
For eutrophication, the exceedance is calculated using total nitrogen deposition (derived from nitrogen oxides and ammonia).
For acidification, the contribution of both sulphur and nitrogen compounds must be taken into account as explained in the methods for calculating the critical loads of acidity above. It is these ‘minimum’ and ‘maximum’ critical loads that are used in the calculation of critical loads exceedance for acidity.
In addition, the “accumulated exceedance” (AE) can be calculated, where exceedance is summed over the whole habitat area:
AE = exceedance * exceeded habitat area
Therefore, the AE is a measure of exceedance that takes into account both the magnitude of exceedance and the habitat area exceeded.
Dynamic Modelling
The current empirical and steady state mass balance critical load methodologies define receptor tolerance to a given pollutant. However, they do not provide information on the response of the receptor to temporal variations in the pollutant, including the periods prior to damage being observed in response to exceedance, and during recovery to reduced pollutant input. There are two factors that can give rise to delays in the cause-effects relationships:
- Biogeochemical processes can delay the chemical response of soils
- Biological processes can further delay the response of indicator organisms, eg damage to trees in forest ecosystems.
Pressure to evaluate the impact of planned reductions in S and N emissions now requires the application of methodologies capable of representing the dynamics of ecosystem change in the above processes. Thus, process-based dynamic models have been developed such as:
- SAFE
- MAGIC
- VSD (Very Simple Dynamic Model).
The evaluation and testing of these models is reliant on the availability of site specific data-sets, including both input parameters required for running the models and, also, output data-sets on which an assessment of the performance of the models can be based. The evaluation and testing of these models can be found in the Terrestrial Umbrella final report.
Useful sites






